Parabolic SAR Strategy
Description
Parabolic SAR (Stop and Reversal) strategy is a trading algorithm which role is to predict market trend change and buy / sell an asset in a specific market conditions. It works well in a bull or bear markets. If a market is neither bear nor bull then SAR coefficient does not have to be helpful and SAR coefficient might be ‘belated’.
Values of all the variables defined in the following paragraphs, except 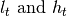 , are not defined for
, are not defined for 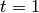 .
.
Lets define by 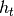 (
(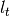 ) the market high (low) at the end of a day
) the market high (low) at the end of a day 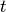 . Moreover,
. Moreover, 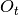 is a strategy’s opinion about market trend at the day
is a strategy’s opinion about market trend at the day 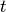 . It has value
. It has value 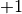 if the opinion is uptrend, and
if the opinion is uptrend, and 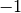 otherwise. It will be formally defined later. To define it precisely (by a math expression) we need first define Extreme Point (
otherwise. It will be formally defined later. To define it precisely (by a math expression) we need first define Extreme Point (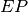 ), Acceletarion Factor (
), Acceletarion Factor (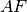 ) and Stop and Reverse (
) and Stop and Reverse (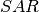 ) variables.
) variables.
A variable 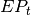 , if
, if 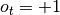 , is the highest value of a high from the beginning of the uptrend. Similarly, if market
, is the highest value of a high from the beginning of the uptrend. Similarly, if market 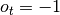 , it is the lowest value of low from the beginning of the downtrend. Formally we can defined it as follows:
, it is the lowest value of low from the beginning of the downtrend. Formally we can defined it as follows:
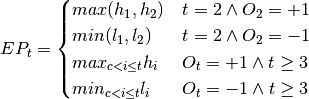
where 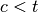 is the biggest value for which
is the biggest value for which 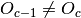 . If there is no such
. If there is no such  (there was no trend change from the time when the strategy starts) then we should set
(there was no trend change from the time when the strategy starts) then we should set  to 1. To sum up: the value of
to 1. To sum up: the value of 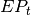 is the highest high or the lowest low of the current trend.
is the highest high or the lowest low of the current trend.
A variable 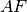 is a kind of a counter which is set to Acceleration Coefficient when the strategy’s opinion about market trend has changed, it is usually equal to 0.02. Moreover it is increased by Acceleration Coefficient when the new extreme value of EP is found (either high or low depending on the strategy’s opinion about market trend). It is worth to mention that its value cannot exceed Acceleration Limit, by default 0.2. Lets define it formally:
is a kind of a counter which is set to Acceleration Coefficient when the strategy’s opinion about market trend has changed, it is usually equal to 0.02. Moreover it is increased by Acceleration Coefficient when the new extreme value of EP is found (either high or low depending on the strategy’s opinion about market trend). It is worth to mention that its value cannot exceed Acceleration Limit, by default 0.2. Lets define it formally:
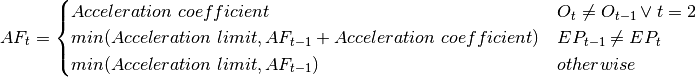
The 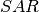 coefficient is defined as a function of its previous value, AF and EP. Formally we can defined it as follows:
coefficient is defined as a function of its previous value, AF and EP. Formally we can defined it as follows:
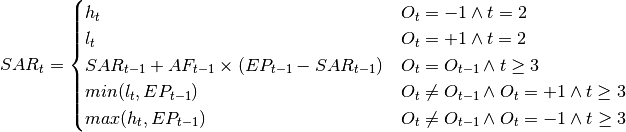
Additionally, when SAR indicator is rising it cannot stay above last two intervals’ low price. When the indicator is falling – it cannot stay below maximum of last two intervals’ high price, either. So, if 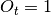 and calculated
and calculated 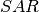 value is bigger than last two periods’ low price (
value is bigger than last two periods’ low price (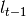 ,
, 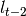 ), then
), then 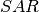 value is set to
value is set to 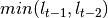 . Analogous, if
. Analogous, if 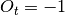 and calculated
and calculated 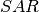 value is smaller than last two periods’ high price (
value is smaller than last two periods’ high price (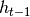 , h_{t-2}), then
, h_{t-2}), then 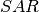 value is set to
value is set to 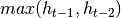 .
.
Finally we can give a formal definition of the 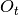 . Its definition is the following:
. Its definition is the following:
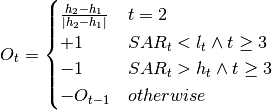 ) we have to determine whether we have an uptrend or downtrend. In above formula fleeting high prices have been used, but this automatic method can be replaced by a parameter Initial Market Trend basing on the user’s opinion.
) we have to determine whether we have an uptrend or downtrend. In above formula fleeting high prices have been used, but this automatic method can be replaced by a parameter Initial Market Trend basing on the user’s opinion.
Market Data
- Last trade
- Historical market data
Parameters
| PARAMETER NAME | DESCRIPTION | ESSENTIAL |
|---|---|---|
| Acceleration Coefficient | Coefficient of acceleration factor, usually set to 0.02 by default | Yes |
| Acceleration Limit | Upper limit of acceleration factor, usually set to 0.2 by default | Yes |
| Initial Market Trend | Initial market trend set arbitrary by an user | No |
Conditions
Open position
Consider day 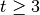 . If strategy does not have an open position and:
. If strategy does not have an open position and:
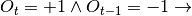 algorithm opens long position
algorithm opens long position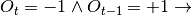 algorithm opens short position
algorithm opens short position
Close position
Consider day 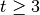 . If strategy does have an open position and:
. If strategy does have an open position and:
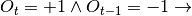 algorithm closes short position
algorithm closes short position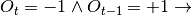 algorithm closes long position
algorithm closes long position
Termination
There is no strategy termination condition.
Time frame
Strategy is designed for long-term trading, usually for whole weeks.
